【はじめに】
　研究計画を立てる際に研究に必要なサンプルサイズをあらかじめ明らかにしておくことは、研究を効率よく実施するために極めて 重要である。しかし、動物実験と人を対象にしたフィールドなどでの疫学研究では、この検討の意味が異なる。
　動物実験では必要な条件を整えれば、サンプルサイズを増やすことは研究の途中からも可能であるのに対して、疫学研究ではいったん 開始した研究のやり直しは極めて困難なので、あらかじめ可能性を検討することは必須の作業である。
　従って実験では研究上必要な標本数の検討は（筆者の経験した範囲では）あまり重視されていない場合が多い。しかし、標本数の追加や、 やり直しは大変な労力を伴うので研究を開始する前に、研究上必要な標本数をあらかじめ見積もっておくことは研究の遂行上有用である 。ここでは効果の検出に用いられる主な検定法を解説し、それぞれの検定法に合った標本数の見積もり方について解説する。

【検定法の種類】
　実験結果の検定法は大きく区分して２種類に分けられる。平均値の比較と率の比較である。一方は連続した値を用いて２群 または３群以上の群間の比較を行う。通常よく用いられる検定法はt-検定や分散分析である。一方率の比較とは２群間で異常値 （この定義は適宜決定するもので絶対的なものではない）の発生率を比較するものである。
　２種類の検定法を比較すると一見平均値の比較の方が有用に見える。しかし、必ずしも平均値の比較の方が有用であるとは限らない。 例えば、異常値を示したため何らかの処置を施したサンプルがある場合など、値そのものでは表せない情報がある場合には率の 検定の方が有用である場合がある。

【平均値の検定】
　平均値の検定は集団間の平均値の差を検討するものである。ここではあるサンプルサイズｎである集団Ｘの検査値 （平均値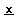）を考えてみよう。この実験を無限回繰り返した場合に、この集団Ｘの 平均値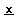はある分布を取るはずである。この分布はｎが小さいほど大きくなり、ｎが 大きくなると分布は小さくなる。この集団における値の平均値のばらつきを標準誤差（SE）といい、以下の式で表すことが出来る。

この実験を無限回繰り返した場合にこの集団の平均値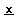が９５％の確率で納まる範囲は

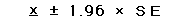
と表すことが出来る。この値の上限と下限の間を95％信頼限界と呼ぶ。最近ではこの値を表示するよう義務づける雑誌も見られる。 標準誤差の検討からわかるように、信頼限界は標本数が大きくなるほど、検討対象となる値の集団内のばらつき（分散）が小さいほど、 小さくなる。つまり値の信頼性が高まって仮説的な母集団の特性を明らかに出来るのである。
　２つの集団の平均値の差を比較したい場合も同様であり、各群内の分散が小さく、標本数が多いほど、２群の平均値の差が大きい ほど平均値の差の検出は容易となる。標本数を少なくするには、平均値の差を大きく、群内の分散を小さくすることが重要なことがわかる。 この集団間の距離の概念がｔ値であると考えると分かりやすい。
　具体的な検定方法としては、２群間の比較で用いられるt-検定（対応のある場合）、主に３群以上で用いられる分散分析がある。 分散分析の考え方については時間があれば解説したい。

【率の検定】
　平均値の差の検定で述べたように、率の場合にも標準誤差という概念が成立する。平均値の差の検定と異なるところは集団内の ばらつきという概念が存在しないことである。同じ50％の陽性率であっても100例観察した場合と、4例の場合では偶然の入る 可能性は大きく異なる。この違いを表現したものが標準誤差と考えて良い。
　観察されたある集団Ｙの陽性率ｙの信頼性は標本数が大きく、観察された陽性の例数が多いほど（陽性率は50％を常に下回る という仮説の元に）高くなる。観察された陽性率ｙの標準誤差は以下の式で示される。

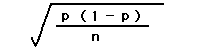
　また平均値の場合と同様に、この実験を無限回繰り返した場合にこの集団の平均値ｘが９５％の確率で納まる範囲は

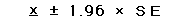
で表すことが出来る。この場合の２つの集団間の率の差の検定にはカイ二乗検定が用いられるが、カイ二乗値とは二つの集団の率 の距離と考えると整理しやすい。統計書にも多く記述があるように、カイ二乗検定を適用するためには、各群の陽性数等に種々の 制限がある。この場合にはFisherの直接確率検定法を用いる必要があるが、最近の統計ソフトではサンプルサイズに応じた検定法を 採用しているので、最終的な検定が何によったかを注意するだけでよい。

【必要な標本数の計算】
　必要な標本数の計算を行う際には第１種のエラー、第２種のエラーについて理解しておくことが必要である。第一種のエラー （α）とは「本来ないはずの差をあると判断してしまう」ことを指し、第二種のエラー（β）とは「本来あるはずの差を検出 できない」ことを指す。どちらのエラーも限りなく０に近いほどよいがその分必要な標本数が幾何級数的に増大する。そこで 現実的な線としてαの確率としてとして５％を与えることが多い。第二種のエラーはαの４倍を取ることが多い。

・平均値の差を検出する場合には下記の式を用いる。

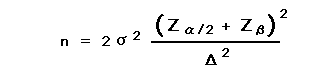
・所見率の差を検出する場合には下記の式を用いる。

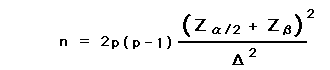
　ここでｚは正規分布表から得られるそれぞれの値を示し、σは変化の標準偏差を示す。Δは変化の予測値である。所見率の 変化の場合には、ｐは２群の平均の有所見率、Δはは有所見率の差である。実際の数字を代入してみると２つの集団に真の差が あればどの様な差であっても、十分な標本数を用意することで検出できる、しかし実際には不可能な標本数になることがわかる。 このようにあらかじめ研究に必要な標本数を計算しておくと、余分な労力が省ける。実際には多くの場合、差の予測が成り立たな い場合も多いが、各種の文献を参考にする際に、データの標準誤差や信頼区間に注意することで推測することが出来る。